DS & A(Queue)

| CHAPTER 14 |

In this chapter, our topic of discussion will be the "Queue" Data Structure. But, before we get started, I would recommend you to read the previous chapters on Data Structures & Algorithms (especially the chapters on Array List, Linked List, Array Stack, and Linked Stack), that is in case it's your first time visiting my blog.

Queue:

• Just like Stacks, Queues also are a restricted version of List but with a few minor differences compared to Stack. The following are some of the notable characteristics of a Queue:
• Data can only be inserted from the rear/back. Data insertion is referred to as ENQUEUE.
• Data can only be deleted from the front. Data deletion is referred to as DEQUEUE.
• Alternatively, ENQUEUE and DEQUEUE should always be executed on the opposite ends of the Queue.
• A Queue follows the FIFO(First In First Out) principle.
• The first and the last elements are referred to as FRONT and REAR respectively.

Visual Representation:

• Array-Based Queue:

• Pointer-Based(Linked) Queue:

Some Theory on Array Based Queue...

As mentioned above a Queue is a restricted version of List so all we need to do is modify the Array-Based list to get our Queue implementation, isn't it? Not actually, If we simply try to implement the Array-Based List to work as an Array-Based Queue the resulting implementation will be kinda inefficient. Why is that? Let's figure that out.

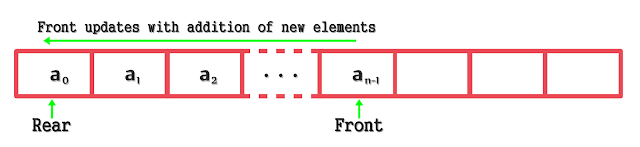
Consider, we have to store n items in a Queue. So, if we try to implement the Queue to work just like an Array-based list then we will need to store those n items in the first n positions of the array, i.e. (0 to n-1). And the Queue will look something like the following.

A Queue has two access points namely FRONT and REAR, we have something analogous to those in an Array List as well, remember HEAD and TAIL?

So, if we try to implement a Queue just like an Array List we would be left with the following two choices:

• Case 1: (ENQUEUE - Rear Shifts Right)

• Case 2: (DEQUEUE - Front Shifts Left)

As mentioned previously implementing a Queue in this manner will be inefficient, but why is it so? Everything feels right, Isn't it? Not actually. To find the issues we have to analyze the ENQUEUE and DEQUEUE operation in both cases.

Case 1 Analysis:

As we already know that ENQUEUE operation is executed from the REAR and DEQUEUE operation is executed from the FRONT. So it can be easily observed that an ENQUEUE operation will require O(1) time only as it is similar to the Append function of the List. But a DEQUEUE operation will require O(n) time, as we will need to shift the remaining n-1 items to the left after removing the element at the FRONT.

Case 2 Analysis:

In Case 2, an ENQUEUE operation will require O(1) time whereas a DEQUEUE operation will require O(n) time, as we will need to shift the pre-existing items to the right before inserting a new element at the REAR.

Solution:

Since both Case 1 and Case 2 are inefficient, we have to approach this problem in a slightly different way, unlike a normal Array-based list. So, we will be making the following changes for a more efficient implementation.

1. Remove the restriction requiring the n queue items to be placed in the first n position of the array. So, the n items of the queue can exist anywhere in the array as long as all the items exist in contiguous array positions.
2. The REAR and FRONT will be arranged as the following. 

3. FRONT and REAR will shift right on DEQUEUE and ENQUEUE respectively and that also in just O(1) time. This implementation will also let us know that the array is empty when REAR<FRONT.

Queue ADT:

1. //Queue.h
2. 
   
3. template<typename e> class Queue
4. {
5.      public:
6.      virtual bool enqueue() = 0;
7.      virtual bool dequeue() = 0;
8.      virtual void print() const = 0;
9. }

Queue Implementation:

• Array Based Queue Implementation

1. //AQueue.h
2. 
   
3. #include"Queue.h"
4. template<typename e> class AQueue:public Queue<e>
5. {
6.     int maxSize;
7.     int front;
8.     int rear;
9.     e* queueArray;
10. public:
11.     AQueue(int sizeValue = 0)
12.     {
13.         maxSize = sizeValue;
14.         rear = 0;
15.         front = 1;
16.         queueArray = new e[maxSize];
17.     }
18.     ~AQueue ()
19.     {
20.         delete [] queueArray;
21.     }
22. 
    
23.     int queueLength()
24.     {
25.         return (rear-front)+1;
26.     }
27. 
    
28.     bool enqueue(const e&);
29.     bool dequeue(e&);
30.     void print() const;
31. };
32. 
    
33. template <typename e>
34. bool AQueue<e>::enqueue(const e& item)
35. {
36.     if (rear == maxSize) return false;
37.     queueArray[++rear] = item;
38.     return true;
39. }
40. 
    
41. template <typename e>
42. bool AQueue<e>::dequeue(e& item)
43. {
44.     if (queueLength() == 0) return false;
45.     item = queueArray[front++];
46.     return true;
47. }
48. 
    
49. template<typename e>
50. void AQueue<e>::print() const
51. {
52.     int tempCounter = front;
53.     std::cout<<"< ";
54.     while(tempCounter <= rear)
55.     {
56.         std::cout<<queueArray[tempCounter]<<" ";
57.         tempCounter++;
58.     }
59.     std::cout<<">";
60. }

• Linked Queue Implementation

1. //Node.h
2. 
   
3. template<typename e> class Node
4. {
5. public:
6.     e element;
7.     Node<e>* next;
8.     Node(e elemVal = 0,Node<e>* nextVal = nullptr)
9.     {
10.         element = elemVal;
11.         next = nextVal;
12.     }
13.     Node(Node<e>* nextVal = nullptr)
14.     {
15.         next = nextVal;
16.     }
17. };

1. //LQueue.h
2. 
   
3. #include"Queue.h"
4. #include"Node.h"
5. #include<iostream>
6. 
   
7. template<typename e> class LQueue : public Queue<e>
8. {
9.     Node<e>* rear;
10.     Node<e>* front;
11.     int size;
12. 
    
13. public:
14.     LQueue()
15.     {
16.         rear = front = nullptr;
17.         size = 0;
18.     }
19. 
    
20.     bool enqueue(const e&);
21.     bool dequeue(e&);
22.     void print() const;
23.     void clear();
24. 
    
25.     int length(){ return size;}
26.     ~LQueue(){clear();}
27. };
28. 
    
29. template<typename e>
30. bool LQueue<e>:: enqueue(const e& item)
31. {
32.     if(rear == nullptr)
33.     {
34.         front = rear = new Node<e>(item,nullptr);
35.     }
36.     else
37.     {
38.         rear->next = new Node<e>(item,nullptr);
39.         rear = rear->next;
40.     }
41.     size++;
42.     return true;
43. }
44. 
    
45. template<typename e>
46. bool LQueue<e>:: dequeue(e& item)
47. {
48.     if(size == 0) return false;
49.     item = front->element;
50.     Node<e>* temp = front;
51.     front = front->next;
52.     delete temp;
53.     if(front==nullptr) rear = nullptr; //if not done rear will be a dangling pointer
54.     size--;
55.     return true;
56. }
57. 
    
58. template<typename e>
59. void LQueue<e>:: print() const
60. {
61.     Node<e>* temp = front;
62.     std::cout<<"< ";
63.     while(temp != rear->next)
64.     {
65.         std::cout<<temp->element<<" ";
66.         temp = temp->next;
67.     }
68.     std::cout<<">";
69.     delete temp;
70. }
71. 
    
72. template<typename e>
73. void LQueue<e>:: clear()
74. {
75.     delete rear;
76.     delete front;
77. }

Testing the Queue implementation

1. //main.cpp
2. 
   
3. #include<iostream>
4. #include"AQueue.h"               //Use this only for testing Array based Queue
5. #include"AQueue.h"               //Use this only for testing Linked Queue
6. using namespace std;
7. 
   
8. int main()
9. {
10.     AQueue<int> newQueue(10);    //Use this only for testing Array based Queue
11.     LQueue<int> newQueue;        //Use this only for testing Linked Queue
12.     newQueue.enqueue(1);
13.     newQueue.enqueue(2);
14.     newQueue.enqueue(3);
15.     newQueue.enqueue(4);
16.     newQueue.enqueue(5);
17.     newQueue.enqueue(6);
18.     newQueue.enqueue(7);
19.     newQueue.enqueue(8);
20.     newQueue.enqueue(9);
21.     newQueue.enqueue(0);
22.     newQueue.print();
23. 
    
24.     int dequeued_element;
25. 
    
26.     int length = newQueue.length(); // initialize newQueue.length() because it's value 
27.                                     // changes with every enqueue or dequeue
28.     cout<<"\n\n";
29.     for(int i = 0; i<length ; i++)
30.     {
31.         newQueue.dequeue(dequeued_element);
32.         cout<<"Removed: "<<dequeued_element<<"\n";
33.     }
34. 
    
35.     return 0;
36. }

Array-Based Queue Implementation: More Issues

If you guys thought that our implementation for the Array-based Queue above is perfect I would have to disappoint you guys cos it still has some daunting issues.

Let's say we have the following Queue and we executed several DEQUEUE operation on it:

---

After the first DEQUEUE

---

---

After the second DEQUEUE

---

---

After the third DEQUEUE

---

I am sure that by this point it's pretty clear that if we use the Array-Based Queue implementation mentioned above then the Queue will become unusable after several ENQUEUE & DEQUEUE operations. So, what's the solution to that problem. Any guess? Don't worry if you can't figure it out, the following section is all about the solution we are looking for.

Circular Queue (aka Circular/Ring Buffer) : The solution

As the name suggests it is a circular Queue Data Structure. But don't get fooled by the name, just because the name contains the term Circular it doesn't mean that the data structure itself is circular, but it's the implementation that makes it behave as if it's circular in nature. We will still be using an Array which is a Linear Data Structure. The following are some of the properties of a Circular Queue implementation.

• FRONT and REAR keeps on getting incremented till it reaches the final index.
• When FRONT is at the last index the next DEQUEUE will move the FRONT to its initial index again. Similarly, when REAR is at the last index the next ENQUEUE will move the REAR to its initial index again.
• A starting empty array slot is necessary. So, a Queue that stores n elements will always require an array of size n+1.

Why do we need the empty array slot?

The empty slot is necessary because of the otherwise possible ambiguity that the circular Queue might encounter. Let's discuss it in detail, Consider the following two cases of circular Queue without an empty array slot.

• Case 1: When the Queue is empty

• Case 2: When the Queue is full

As you can see from Case 1 and Case 2 that if the empty array slot in the Queue implementation is not present then a full and an empty Queue cannot be distinguished leading to an ambiguous scenario. So, the empty array is mandatory in a Circular implementation.

Circular Queue Implementation:

I leave it to you guys as an exercise. Try implementing it. All the best...

OR

You can join our Facebook group for the code

( If you like the content here, follow TSP on social media to get notified on future updates)